•   Blog   •   Control Flow in Haskell (3) - Flow with Variant

Control Flow in Haskell (3) - Flow with Variant
Tags: Haskell, Control Flow, Variant December 12, 2016

This post is part of a series.

Control flow with Variant

We can use the Variant data type described in the previous part to help with control flow. Basically we can write functions that return a Variant to indicate their different possible output types. To make the code easier to read (fewer brackets), we use the following type alias:

Here is our previous example from part 1 rewritten to use Flow:

Notice how the same error types (such as ErrA) can be returned by different functions without being wrapped with different constructors each time.

Another thing to notice is that all the return types are at the same level: there is no difference between “success” types and “error” types. Compared to using Either Errors UV, we avoid the indirection caused by the Errors sum type.

Similarly to Either, however, we can have a convention about the most expected returned type. With Either a b we most expect the type associated to the Right constructor (i.e., b); with Variant (x ': xs) we most expect the first type in the list (i.e., x). This is useful to define composition operators on variants such as >.~^^> in the code above (operators are presented in the next section).

Flow operators

There are many ways to compose flows. Say we have the following function:

There are many potential g functions that we would like to compose with f to get the h functions.

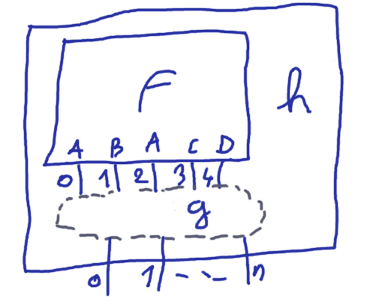
(It’s the first time I use a graphics tablet: it is much faster to draw things but I’m not very good at it)

Moreover, we need to make the types unambiguous without having to add type annotations everywhere, especially for intermediate values. So we have different operators with different type dependencies: f -> g h, f g -> h, h f -> g, etc.

Returning a value

Let’s start with the value returning “operators”:

First output biased operators

We have said that by convention the first output type in the type list is the most expected one (equivalent to the Right constructor for Either). So we have a bunch of operators biased for this case.

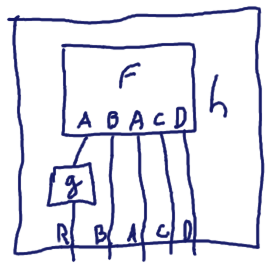
First, the equivalent of fmap for Flows (g is pure):

The equivalent of forM/traverse for Flows (g is monadic in the same Monad as f):

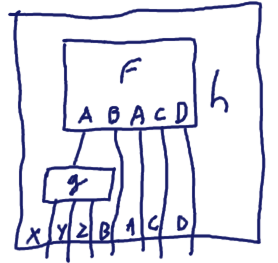
When g has several output types and output types are concatenated:

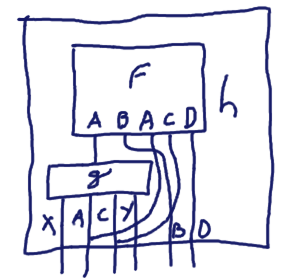
When g has several output types, f and g determine the output types of h (by union):

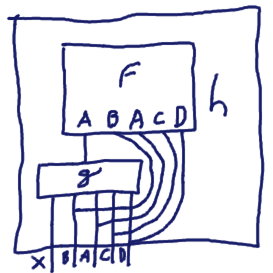
When g has several output types (the same as f except for the first one):

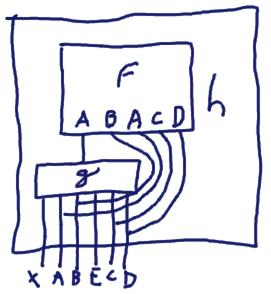
When g has several output types, g determines the output types of h:

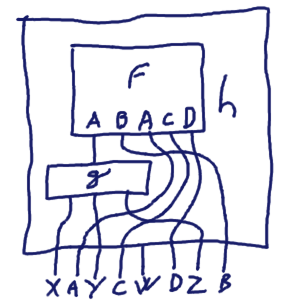
When g has several output types, h determines its own output types:

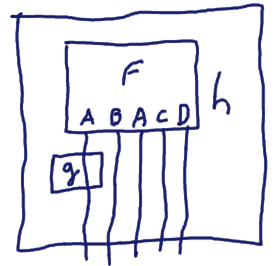
When g only performs some effects:

When g only performs some effects: this one is a little bit more suspicious (hence the !) because some output paths are not explicitly handled:

When g only performs some effects: this case is even more dangerous because you assert that the first output path mustn’t be followed. g mustn’t return (i.e., it should call error for instance).

Other operators

The operators presented in the previous sections are biased towards the first output but we also have other operators for other cases! To avoid having to learn each operator, here is the logic I have followed to build them. Operators are decomposed in three parts:

  • what we select in the Variant:
    • . the head
    • .. the tail
    • % a mandatory type
    • ? an optional type
    • ..% a mandatory type in the tail
    • ..? an optional type in the tail
  • what kind of function we apply to it:
    • - pure function
    • ~ monadic function
    • ~~ constant monadic function (doesn’t use its parameter)
  • how we combine the result p with the remaining part q to get the result r:
    • + r = concatenate p and q
    • . set the head of the result (p isn’t a Variant in this case)
    • | r = union of p and q
    • ^ lift q into p, r = p
    • ^^ lift p and q into r
    • $ tail r = tail p = tail q
    • = perform an effet and passthrough the Variant
    • ! perform an effect and return ()
    • !! perform a bottom effect or return q

By combining these three parts, we have operators such as: >..~.>, >..~^>, >..~!!>, >%~.>, >%~^>, >%~!!> >..%~.>, >..%~^>, >..%~!!>, >?~!>, >..?~!!, etc. The full list is in the Flow module in my haskus-system package.

Note that in some cases, the combination of the parts doesn’t make sense. Also in some cases I have replaced Flow m '[x] with m x as it is easier to work with.

Examples

Consider the following example where we have a function f that may return either an A, a B or a C.

Now, if we want to do something if a C is returned, we can use the >%~!> operator as follows.

Now suppose that we want to do something if a D is returned:

Oops, we get the following error:

scripts/Flow.hs:27:4: error:
    • `D' is not a member of '[A, B, C]
    • In a stmt of a 'do' block:
        f 2 >%~!> \ (d :: D) -> putStrLn "  -> D returned!"

Indeed f never returns a D and the compiler checks that.

Note that it is possible to write generic functions that take as parameters functions that may or may not return some types. For instance by using the >?~!!> operator as the handleD function does in the following code:

Pattern-matching and Flows

Sometimes we would like to use pattern matching instead of using a sequence of fish operators like the following one:

We can do something similar with flowToCont and the >::> operator. In this case the continuations are matched by position in the tuple:

We can also match them by type if there is no ambiguity with the >:%:> operator:

Continuations like this will be the topic of a planned next part.